Research

I am engaged in research to develop machine learning theory based on information geometry. My background in master’s course was physics. So I am intensely interested in the interdisciplinary academic field of intelligent informatics and physics. When I can describe things in machine learning with physics terms, I am thrilled.

機械学習の理論寄りの研究に取り組んでいます．特に情報幾何学を用います．修士号は物理学で取りました．そのため，機械学習と物理学の学際的な部分に興味があります．特に，物理の言葉で機械学習を説明することに関心があります．

Many-body approximation for tensors

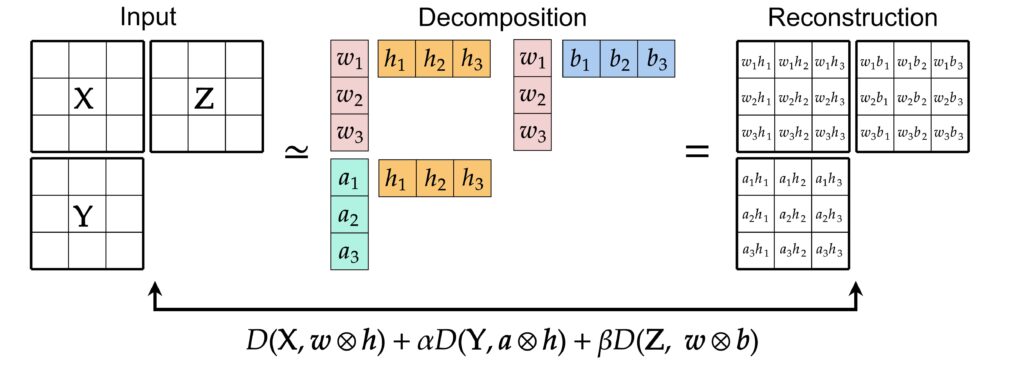
Faster rank-1 NMF with missing values

Nonnegative multiple matrix factorization (NMMF) is the task of decomposing multiple nonnegative matrices by shared factors. We have derived a closed formula of the best rank-1 NMMF when the cost function is defined by KL divergence. Using this solution formula, we proposed A1GM, a faster method to find approximate solutions of rank-1 NMF when the input matrix has missing values.

非負複合行列因子分解(NMMF)は，複数の非負行列を共有因子で分解するタスクです．私たちは，コスト関数をKL情報量で定義する場合の，NMMFの最良ランク１分解の公式を，情報幾何学的な議論により導出しました．この解の公式を用いて，入力行列が欠損を含む場合のランク１NMFの近似解を高速に求める手法A1GMを提案しました．

Related papers
– K.Ghalamkari, et al., “Fast Rank-1 NMF for Missing Data with KL Divergence” presented in AISTATS2022.
– K.Ghalamkari, et al., “Non-negative low-rank approximations for multi-dimensional arrays on statistical manifold” pubulished in Information Geometry (Springer)

Tensor low-rank approximation

Tensor low-rank approximation is the task of approximating a tensor (multidimensional array) with a low-rank tensor. To date, most low-rank approximation methods are based on gradient descent using the derivative of the cost function, which often requires careful tuning of initialization, learning rate, and a tolerance threshold. By mapping tensors to probability distributions and applying the theory of projection in information geometry, we have developed Legendre Tucker Rank Reduction (LTR), a fast non-negative low-rank approximation method that is not based on the gradient method.

From the viewpoint of information geometry, we also explain that we can regard the rank-1 approximation as a mean-field approximation because the probability distribution corresponding to the rank-1 tensor is expressed as a product of independent distributions.

テンソル（多次元配列）をランクの低いテンソルで近似するタスクがテンソル低ランク近似です．従来，この低ランク近似は，入力テンソルと低ランク近似後のテンソルの誤差を小さくする勾配法によって行われてきました．しかし，勾配法に基づく手法は，適切な初期値や収束判定，学習率の設定などのチューニングが必要です．私たちは，テンソルを確率分布と対応付け，情報幾何学の射影の理論を活用することで，勾配法に基づかない非負テンソルの高速な低ランク近似手法Legendre Tucker Rank Reduction(LTR)を開発しました．

また，ランク１テンソルに対応する確率分布が独立分布の積として表現できるため，ランク１近似を平均場近似として理解できることを情報幾何学的な観点から説明しました．

Related papers
– K.Ghalamkari, et al., “Fast Tucker Rank Reduction for Non-Negative Tensors Using Mean-Field Approximation” presented in NeurIPS2021.
– K.Ghalamkari, et al., “Non-negative low-rank approximations for multi-dimensional arrays on statistical manifold” pubulished in Information Geometry (Springer)

Valley polarization in layer material by light absorption

I received my master’s degree in theoretical condensed matter physics in hexagonal lattice systems such as graphene, h-BN, Silicene, and Stanene.

Hexagonal lattice systems, in which two atoms in a unit cell are different atoms, have K valleys and K’ valleys in the Brillouin zone. It is known that the electrons in the K(K’) valleys are excited when left (right) circularly polarized light is incident in this system. The system is said to be valley polarized when there is a bias in which valley electrons are more likely to be excited depending on the polarization state of the irradiated light. I have analytically demonstrated valley polarization in a hexagonal lattice system consisting of atoms with complex electronic orbitals such as TMDs [1]. We also provide an analytical explanation of how the valley polarization varies with the energy band gap and incident energy [2].

Furthermore, I have clarified the relationship between band inversion and valley polarization by studying the presence or absence of valley polarization in the Haldane model [3].

グラフェン、h-BN、シリセン、スタネンなどの六角形格子系における物性物理学(理論)で修士号を取得しました。

単位胞ユニットセル内の2つの原子が異種である六方格子系はブリルアンゾーン内にKバレー,K’バレーを有します。この系に左（右）円偏光を入射するとK(K’)バレーの電子が励起されることが知られています．照射する光の偏光状態に応じてどちらのバレーの電子が励起しやすいかという偏りがある場合に「系にバレー偏極が生じている」と言います．このバレー偏極の解析的な議論で修士号を取得しました．TMDsなど複雑な電子軌道をもつ原子からなる六角格子系のバレー偏極を解析的に示しました[1]。またバレー偏極がどのくらい生じているのかを表す指標として定義されるバレー偏極度がエネルギーバンドギャップや入射するエネルギーに対してどのように変化するのかについて解析的な説明を与えました[2].

さらに、Haldaneモデルにおけるバレー偏極の有無を調べることで、バンド反転とバレー偏極の関係を明らかにしました[3]．

[1] Y.Tatsumi, et al. Laser energy dependence of valley polarization in transition-metal dichalcogenides, Phys. Rev. B 94, 235408 (2016) 
[2] K.Ghalamkari, et al. Energy Band Gap Dependence of Valley Polarization of the Hexagonal Lattice, J. Phys. Soc. Jpn. 87, 024710 (2018)
[3] K.Ghalamkari, et al. Perfect circular dichroism in the Haldane model, J. Phys. Soc. Jpn. 87, 063708 (2018)